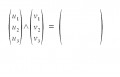2392 shaares
51 results
tagged
maths
Une belle animation décrivant une technique de calcul du produit vectoriel en physique.
Application du théorème de Slutsky pour démontrer qu'une variable centrée et réduite multipliée par sqrt(n) converge en distribution vers une loi normale centrée et réduite quand n tend vers l'infini.
Intéressant
Un outil en ligne pour intégrer une expression. Super utile!
En nettoyant mes mails. je retombe sur ce joyau: la preuve mathématique que 1+1=2.
Des fois, les matheux exagèrent...
Des fois, les matheux exagèrent...
Ah bon, ya ce package de Martin Mächler sous R qui permet de faire des calculs en précision arbitraire. Bon ben je sais pas pourquoi je cherche ailleurs, ya vraiment tout sous R...
Pour faire des calculs en précision arbitraire sous linux. Bon, je ne sais pas trop dans quel contexte je pourrais en avoir l'usage, mais on ne sais jamais, à garder sous le coude.
Dans quelles conditions une somme de Bernoulli converge vers une Poisson LORSQUE LES BERNOULLI NE SONT PAS NÉCESSAIREMENT IDENTIQUEMENT DISTRIBUÉS!!!!!
Ça, c'est de l'inégalité utile!
Ça, c'est de l'inégalité utile!
La date d'aujourd'hui correspond à un nombre premier, et ce, quel que soit le format d'écriture de la date.
Bon.
D'accord.
Bon.
D'accord.
Apprendre à multiplier à la japonaise. C'est assez efficace.
Mais d'après imgur, ce serait plutôt du coréen, mais bon. C'est tout aussi efficace
Mais d'après imgur, ce serait plutôt du coréen, mais bon. C'est tout aussi efficace
L'explication des multiplicateurs de Lagrange sur Wikipédia, c'est clair comme du cristal: non seulement ils expliquent bien comment ça marche, mais encore pourquoi ça marche!
Edit: Cela dit, le livre de Nocedal & Wright sur l'optimisation sous contraintes est plus complet, et encore plus clair, puisqu'ils considèrent également le cas où les contraintes contiennent aussi des inégalités.
Edit: Cela dit, le livre de Nocedal & Wright sur l'optimisation sous contraintes est plus complet, et encore plus clair, puisqu'ils considèrent également le cas où les contraintes contiennent aussi des inégalités.