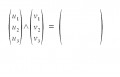2394 shaares
Très intéressant: apparemment certaines photos de Mary Winstead avaient été supprimées. Comme l'indique le journaliste il y a deux options: (i) soit le pirate compile ses photos ça depuis plusieurs années, (ii) soit Apple ne supprime pas les photos quand on le lui demande... L'option (ii) ne me paraît pas la moins probable: elle implique que quand on prend une photo, elle finit chez apple, et reste chez apple. Curieux, hein?
Bon, rien de sûr, mais dans tous les cas, la leçon que j'en retiens: il faut impérativement éviter les services de Cloud tant qu'on peut.
Mais ça je savais déjà.
Bon, rien de sûr, mais dans tous les cas, la leçon que j'en retiens: il faut impérativement éviter les services de Cloud tant qu'on peut.
Mais ça je savais déjà.
M'a l'air intéressant. À lire
Bon, et puis je stocke ce post ici, il semble être un peu incontournable en ce moment, et tout le monde en parle, surtout depuis la présentation de Ben Bolker à l'ISEC à Montpellier. La notion de machisme statistique décrit la tendance à vouloir écraser le lecteur sous un arsenal monstrueux de statistiques compliquées et incompréhensibles. C'est ce bloggeur qui a introduit la notion, et qui est très à la mode en ce moment en écologie.
Un peu d'éthymologie:
Courbe sigmoïde: ça vient de la lettre grecque sigma qui produit le son S, et S est la forme de la courbe. Zont été la chercher loin celle-là.
Logarithme: vient de logos (rapport, proportion) et arithmos (nombre), inventé par John Napier au XVIème siècle.
Logistique: inventé par Verhulst au XIXème siècle, sans raison, mais apparemment, en grec ça veut dire calcul, et jusqu'au XVIIIème logistique était synonyme de logarithme. Plus après Verhulst.
Me coucherai moins con.
Courbe sigmoïde: ça vient de la lettre grecque sigma qui produit le son S, et S est la forme de la courbe. Zont été la chercher loin celle-là.
Logarithme: vient de logos (rapport, proportion) et arithmos (nombre), inventé par John Napier au XVIème siècle.
Logistique: inventé par Verhulst au XIXème siècle, sans raison, mais apparemment, en grec ça veut dire calcul, et jusqu'au XVIIIème logistique était synonyme de logarithme. Plus après Verhulst.
Me coucherai moins con.
Comment calculer l'espérance d'une distribution gamma.
Et ça chauffe dans les commentaires. Parmi les réponses, Marc kéry, Darryl Mackenzie. À lire.
Il faut y arrêter avec les méthodes super-compliquées.
Edit: OK, j'ai vu la vidéo, le message est plus nuancé: la question est de savoir si ça vaut vraiment la peine de se lancer dans les nouvelles méthodes à la mode. Du point de vue du statisticien, le développement de nouvelles méthodes est aussi un moyen de publier. Et pour faciliter la publication, il va probablement souligner l'utilité du machin. La question est de savoir si ça vaut vraiment le coût. En fait si c'est une machinerie monstrueuse pour une amélioration de 5%, ce n'est pas la peine ("not worth the trouble"). Et Bolker dit un truc très juste: on passe son temps à se faire emmerder par des référés sur "vous auriez dû utiliiser telle méthode, etc.". Bolker remarque qu'il y a trois types de référés: (i) ceux qui ne connaisse rien aux statistiques et qui ne vont pas nous emmerder là-dessus, (ii) ceux qui s'y connaissent bien, et qui vont relire le matériel stat, juger de la pertinence des choix et accepter ceux qui ne sont légèrement suboptimaux sans forcément bouler le papier, et (iii) ceux qui connaissent suffisamment de stats pour savoir que la méthode X aurait aussi été pertinente, mais pas assez pour savoir que l'application de cette méthode n'aurait apporté qu'une très légère amélioration par rapport aux résultats obtenus. Et ces derniers sont les plus chiants.
Edit: OK, j'ai vu la vidéo, le message est plus nuancé: la question est de savoir si ça vaut vraiment la peine de se lancer dans les nouvelles méthodes à la mode. Du point de vue du statisticien, le développement de nouvelles méthodes est aussi un moyen de publier. Et pour faciliter la publication, il va probablement souligner l'utilité du machin. La question est de savoir si ça vaut vraiment le coût. En fait si c'est une machinerie monstrueuse pour une amélioration de 5%, ce n'est pas la peine ("not worth the trouble"). Et Bolker dit un truc très juste: on passe son temps à se faire emmerder par des référés sur "vous auriez dû utiliiser telle méthode, etc.". Bolker remarque qu'il y a trois types de référés: (i) ceux qui ne connaisse rien aux statistiques et qui ne vont pas nous emmerder là-dessus, (ii) ceux qui s'y connaissent bien, et qui vont relire le matériel stat, juger de la pertinence des choix et accepter ceux qui ne sont légèrement suboptimaux sans forcément bouler le papier, et (iii) ceux qui connaissent suffisamment de stats pour savoir que la méthode X aurait aussi été pertinente, mais pas assez pour savoir que l'application de cette méthode n'aurait apporté qu'une très légère amélioration par rapport aux résultats obtenus. Et ces derniers sont les plus chiants.
Sur la distribution gamma. Le paramètre beta est un paramètre d'échelle (scale), et il est parfois utile de le fixer égal à 1. On parle alors de la forme standard de la distribution gamma (standard form, standard gamma, etc.). Voir aussi Johnson et al. (1995, continuous univariate distribution, volume 1, p. 337, équation 17.2).
À noter aussi: sous R comme sous JAGS, par défaut le paramètre contrôlant ce "scaling" est le taux (rate) = 1/paramètre d'échelle. Et par défaut, ce paramètre vaut 1 sous R.
À noter aussi: sous R comme sous JAGS, par défaut le paramètre contrôlant ce "scaling" est le taux (rate) = 1/paramètre d'échelle. Et par défaut, ce paramètre vaut 1 sous R.
Tout ce que vous avez toujours voulu savoir sur la loi binomiale négative sans jamais oser le demander
Une autre solution au slicer coincé à l'infini. Et une explication au problème...
grrrrrr
Edit: si le problème se produit, il ne faut pas oublier que la distribution gamma inclue une *fonction* gamma, et que Gamma(x) = (x-1)!
Et la factorielle augmente assez fortement avec x. Donc pour une distribution gamma G(a,b), si a est trop important, Gamma(a) ne pourra être calculé numériquement, et ça se traduira par une valeur infinie. Un bidouillage consiste à tronquer la prior de a si a est une variable à estimer.
grrrrrr
Edit: si le problème se produit, il ne faut pas oublier que la distribution gamma inclue une *fonction* gamma, et que Gamma(x) = (x-1)!
Et la factorielle augmente assez fortement avec x. Donc pour une distribution gamma G(a,b), si a est trop important, Gamma(a) ne pourra être calculé numériquement, et ça se traduira par une valeur infinie. Un bidouillage consiste à tronquer la prior de a si a est une variable à estimer.
La loi gamma est une loi de merde. Mais malheureusement, parfois inévitable.
Intéressant: les 7 piliers de la sagesse statistique d'après Stigler.
il existe une différence entre nombres pseudo-aléatoires (ceux que l'on utilise dans R), et nombres quasi-aléatoires, qui construisent les séquences à discrépance faible (la discrépance d'une suite est faible si la proportion des points de la suite sur un ensemble B est proche de la valeur de la mesure de B, ce qui est le cas en moyenne (mais pas pour des échantillons particuliers) pour une suite équidistribuée). On s'en sert parfois pour remplacer les nombres pseudo-aléatoire
Une thèse. Paraitrait qu'elle est pas mal.
Plein d'alias rigolo pour bash
Une belle animation décrivant une technique de calcul du produit vectoriel en physique.
Poisson d'avril? Sinon, ça craint vraiment.
via le hollandais volant.
via le hollandais volant.
Je me stocke ça ici pour si jamais un jour je retombe sur le même problème. Quand on ajuste un modèle de tendance temporelle avec des résidus autocorrélés selon un modèle de corrélation exponentielle (Diggle et al. 2002, Analysis of longitudinal data, p. 56) avec JAGS, il ne faut pas générer les résidus en tirant dans une loi multinormale de moyenne nulle que l'on va ajouter à une tendance. Il faut tirer dans une loi multinormale dont le vecteur moyenne EST la tendance. Je me suis arraché les cheveux là-dessus, mais le mélange est bien meilleur si l'on procède comme ça. Autrement dit, il ne faut pas faire ça:
residus~dmnorm(vecteurDeZeros, Omega)
for (i in 1:10) {
esperance[i]<- mu[i] + residus[i]
}
Mais plutôt faire ça:
esperance~dmnorm(mu, Omega)
Les chaînes se mélangent mieux. Fallait le savoir...
Edit: Bon apparemment, la stratégie est connue et est valable pour tout modèle linéaire réclamant un résidu quelconque: on ne doit jamais tirer au sort un résidu dans une loi normale de moyenne nulle. Mais on indique que la réponse suit une loi normale de moyenne correspondant à l'espérance modélisée. Ça s'appelle du hierarchical centring (voir Browne et al. 2009, dans Journal of the Royal Statistical Society). Par contre, il paraît que ça marche pas top quand la variance est faible.
residus~dmnorm(vecteurDeZeros, Omega)
for (i in 1:10) {
esperance[i]<- mu[i] + residus[i]
}
Mais plutôt faire ça:
esperance~dmnorm(mu, Omega)
Les chaînes se mélangent mieux. Fallait le savoir...
Edit: Bon apparemment, la stratégie est connue et est valable pour tout modèle linéaire réclamant un résidu quelconque: on ne doit jamais tirer au sort un résidu dans une loi normale de moyenne nulle. Mais on indique que la réponse suit une loi normale de moyenne correspondant à l'espérance modélisée. Ça s'appelle du hierarchical centring (voir Browne et al. 2009, dans Journal of the Royal Statistical Society). Par contre, il paraît que ça marche pas top quand la variance est faible.
Marrant